Sur un travail de Jacques Lubczanski (tonton lulu)
- le pdf
\PassOptionsToPackage{np}{numprint}
\documentclass{scrartcl}
\KOMAoptions{paper=a4, fontsize=11pt}
\usepackage[exos]{matha}
\usepackage{tkz-fct, tkz-tukey}
\usepackage{setspace,spreadtab,tabularx}
\rfoot{\textbf{Page \thepage\ sur \pageref{LastPage}}\\ \tiny{\today}}
\entete{Travail personnel }{Repérage triangulaire}
\setlength{\textwidth}{509pt}
\setlength{\hoffset}{-35pt}
\begin{document}
\subsection*{On est foutus, on mange trop! (et mal?)}
Parmi les
critères utilisés pour analyser la qualité de ce que nous mangeons, la
répartition en glucides, protides et lipides fournit une première approche. En
effet les substances nutritives contenues dans un aliment se répartissent en
trois groupes: les glucides ("sucres", {\it énergétiques}), les protides ("matières azotées", {\it constituant des muscles et cellules}) et
les lipides ("graisses", {\it stockage}). A chaque aliment correspond donc une répartition en
pourcentages : par exemple les épinards contiennent $55$\% de glucides, $40$\%
de protides et $5$\% de lipides.\medskip
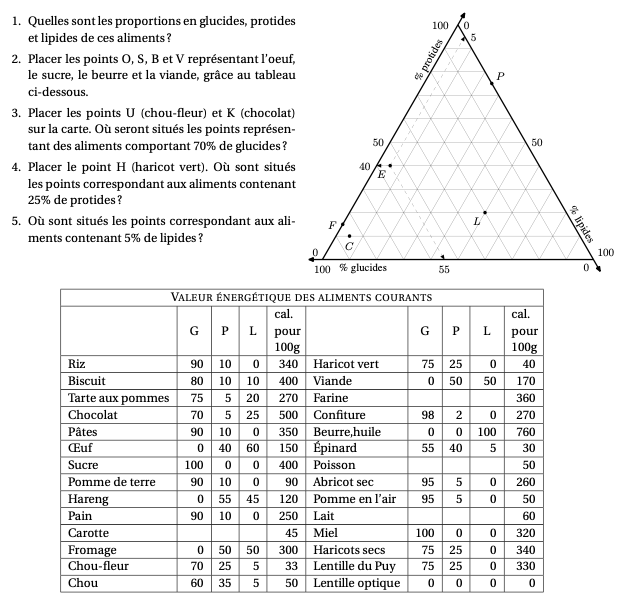
{\bf La "carte" des aliments.}\\
Dans cette partie, on va dresser une carte des principaux aliments,
c'est-à-dire établir un graphique où chaque aliment est représenté par un
point.
\`A titre d'exemple, le point $E$ représentant les épinards a été dessiné.
On dira que le point $E$ a pour coordonnées $(55;40;5)$.
Pour lire les coordonnées $(G;P;L)$ d'un point quelconque du graphique, il faut
tracer des parallèles aux axes passant par ce point.
Cette construction a été faite pour le point $E$ sur la carte des aliments.
Sur cette carte figurent aussi les points $L$, $C$, $F$ et $P$ représentant le
lait, la carotte, la farine et le poisson.
\begin{multicols}{2}
\begin{enumerate}
\item Quelles sont les proportions en glucides, protides et lipides de
ces aliments?
\item Placer les points $O$, $S$, $B$ et $V$ représentant l'oeuf, le sucre,
le beurre et la viande, grâce au tableau ci-dessous.
\item Placer les points $U$ (chou-fleur) et $K$ (chocolat) sur la carte.
Où seront situés les points représentant des aliments comportant 70\%
de glucides?
\item Placer le point $H$ (haricot vert). Où sont situés les points
correspondant aux aliments contenant 25\% de protides?
\item Où sont situés les points correspondant aux aliments contenant 5\% de
lipides?
\end{enumerate}
\begin{center}
\includegraphics{figure.1}
\end{center}
\end{multicols}
\begin{center}
\begin{tabular}{|*{2}{l|*{4}{r|}}}\hline
\multicolumn{10}{|c|}{\sc Valeur énergétique des aliments courants}\\\hline
\multicolumn{1}{|c|}{}&
\multicolumn{1}{c|}{G}&
\multicolumn{1}{c|}{P}&
\multicolumn{1}{c|}{L}&
\multicolumn{1}{m{.7cm}|}{cal. pour 100g}&
\multicolumn{1}{c|}{}&
\multicolumn{1}{c|}{G}&
\multicolumn{1}{c|}{P}&
\multicolumn{1}{c|}{L}&
\multicolumn{1}{m{.7cm}|}{cal. pour 100g} \\\hline
Riz&90&10&0&340&Haricot vert&75&25&0&40 \\\hline
Biscuit&80&10&10&400&Viande&0&50&50&170 \\\hline
Tarte aux pommes&75&5&20&270&Farine&&&&360 \\\hline
Chocolat&70&5&25&500&Confiture&98&2&0&270 \\\hline
Pâtes&90&10&0&350&Beurre,huile&0&0&100&760 \\\hline
\OE{}uf&0&40&60&150&\'Epinard&55&40&5&30 \\\hline
Sucre&100&0&0&400&Poisson&&&&50 \\\hline
Pomme de terre&90&10&0&90&Abricot sec&95&5&0&260 \\\hline
Hareng&0&55&45&120&Pomme en l'air&95&5&0&50 \\\hline
Pain&90&10&0&250&Lait&&&&60 \\\hline
Carotte&&&&45&Miel&100&0&0&320 \\\hline
Fromage&0&50&50&300&Haricots secs&75&25&0&340 \\\hline
Chou-fleur&70&25&5&33&Lentille du Puy&75&25&0&330 \\\hline
Chou&60&35&5&50&Lentille optique&0&0&0&0 \\\hline
\end{tabular}
\end{center}
\pagebreak
{\bf La zone idéale.}\medskip
On note $G$, $P$ et $L$ les proportions en pourcentages d'un aliment quelconque.\medskip
\begin{enumerate}
\begin{minipage}{0.44\textwidth}
\item Placer sur le graphique ci-dessous le point $R$
(riz, pomme de terre,
pain et pâtes).
Où se trouvent les aliments tels que $P>10$?
(Hachurer la région qui ne convient pas).
\item Résoudre graphiquement: $P<20$, puis $G<60$.
\item Les diététiciens ont établi que les proportions en glucides, protides et
lipides les mieux adaptées\ldots
\end{minipage}\hfill\begin{minipage}{0.43\textwidth}
\ldots à l'homme vérifient :
$10<P<20$; $50<G<60$; $25<L<35$.
Déterminer la région correspondante du graphique. Reporter le contour de
cette \og zone idéale\fg sur la carte des aliments.
\item Quels aliments se trouvent à l'intérieur de cette zone?
\end{minipage}
\end{enumerate}
\medskip
{\bf Où commence la cuisine.}\medskip
Le principe est le suivant: en mélangeant les aliments, arriver à ce que les
proportions $G$, $P$ et $L$ du mélange soient dans la zone idéale.
\begin{multicols}{2}
\begin{enumerate}
\item \textsl{Le gâteau breton \og quatre-quarts\fg.}
La recette en est simple:
un quart de sucre, un quart de farine, un quart de beurre,
un quart d'oeuf (les quarts sont comptés en masses).
\begin{enumerate}
\item Quelles sont les coordonnées $(G,P,L)$ du point $Q$ représentant le
quatre-quarts?
\item Construction géométrique du point $Q$: soit $M_1$ le milieu de
$[BS]$ et $M_2$ le milieu de $[FO]$.
Quelles sont les coordonnées $M_1$ et $M_2$?
Montrer que $M_1$ représente un mélange à parts égales de beurre et de sucre.
Que peut-on dire de $M_2$?
En déduire une construction géométrique simple de $Q$.
\item $Q$ n'est pas dans la zone idéale: comment peut-on modifier la recette pour qu'il y soit?
\end{enumerate}
\item \textsl{Le petit déjeuner.}
\begin{enumerate}
\item Montrer qu'une tartine de pain beurré n'est jamais dans la zone idéale.
Et si on ajoute du chocolat? de la confiture?
\item Représenter le mélange constitué d'une tartine beurrée (50g de pain,
10 g de beurre) et d'un verre de lait (6 g de lait):
est-il dans la zone idéale? Et si on remplace le lait par du fromage?
\end{enumerate}
\item \textsl{\`A vous de choisir!}
Sachant que l'apport calorique journalier moyen d'un adolescent est de 3\,000 calories pour les garçons et de 2\,500 calories pour les filles, composez un menu de votre choix (petit déjeuner, déjeuner, goûter, souper). Calculez les coordonnées de la somme des aliments
de la journée. Votre alimentation est-elle dans la zone idéale?
\item \textsl{Et les fast-food}
Le repas est en général constitué d'un hamburger (35g de pain, 35 g de
viande), de frites (90g de pommes de terre et 10g d'huile) et d'un
coca-cola (20g de sucre).
Placer sur la carte le point $D$ représentant ce repas. Est-il dans la zone
idéale? Conclure.
\end{enumerate}
\end{multicols}
\begin{center}
\includegraphics{figure.2}
{\small \gray \copyright\,Les trésors de Tonton Lulu, Jacques Lubczanski}
\end{center}
\end{document}